La gente comenzó a usar números hace mucho tiempo. Para ello, utilizaron principalmente los dedos de sus manos. Las personas simplemente mostraron con los dedos la cantidad de objetos que querían reportar. Entonces, los nombres de los números surgieron y se fueron consolidando gradualmente: 1, 2, 3, 4, 5, 6, 7, 8, 9. ¿Y qué pasa si hay más objetos que dedos? Luego tuve que mostrar mis manos varias veces, lo que, por supuesto, no se adaptaba a todos. Y luego los hombres inteligentes, ya sea en India o en el mundo árabe, encontraron otro número: cero, lo que significa la ausencia de objetos, y con ello el sistema numérico decimal. El decimal es porque se usan diez números:0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . 
Sistema de numeración numérica y decimal
Los números difieren de los números en quepuede consistir en uno o varios números registrados en una fila . El sistema numérico decimal es un sistema posicional. El valor de un dígito depende del lugar (posición) que ocupa en el número. Los números también son números, pero consisten en un dígito, que ocupa una posición en la descarga de unidades. Si necesita escribir el número siguiente en orden de 9, debe pasar a la siguiente categoría: las decenas.
Por lo tanto, el siguiente número será 10: una decena, cero unidades, 11: una, diez una unidad, 12: una, diez, dos unidades, 25: dos docenas de cinco unidades y así sucesivamente. Después del número 99 viene el número 100: cien cero docenas de unidades cero. Luego se agregan las filas de miles, decenas de miles, cientos de miles, millones, etc. Así, al agregar nuevos rangos a la izquierda, podemos usar más y másgrandes numeros
Números fraccionarios
Desde el recálculo de objetos, que se lleva a cabo con la ayuda de números naturales, la humanidad, naturalmente, pasó a contar las medidas de longitud, peso y tiempo. Y luego estaba el problema de cómo contar partes no integrales. Las fracciones naturales aparecieron naturalmente: mitad, tercero, cuarto, quinto, etc. Comenzaron a escribir en la forma del numerador y el denominador: el denominador se registró en cuántas partes se divide el conjunto y en el numerador, cuántas partes se toman. Por ejemplo, la mitad es 1/2, el tercero es 1/3, el cuarto es 1/4, etc.
Fracciones decimales
Dado que la humanidad utilizó cada vez más el sistema numérico decimal, para reducir los registros de números fraccionarios a la forma decimal, fracciones con denominadores en forma de unidades de bits 10, 100, 1000, 10 000, etc. Comenzó a escribir en forma de fracciones decimales, donde la parte fraccionaria se separó de toda la coma o punto. Por ejemplo, 1/10 = 0.1, 1/100 = 0.01, 1/1000 = 0.001, 1/10000 = 0.0001. Además, las fracciones convencionales comenzaron a convertirse en decimales al dividir el numerador por el denominador, y si el reemplazo exacto fallaba, se hacía aproximadamente, con la precisión que satisfacía las necesidades prácticas de las personas. 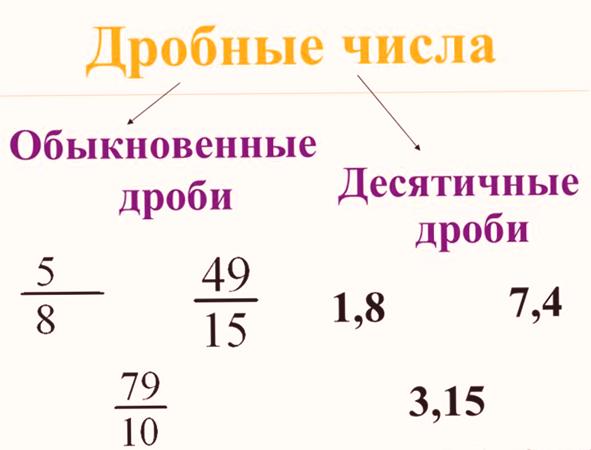
Números romanos
No es necesario pensar que el número decimal al que estamos acostumbrados, con diez dígitos, se usó siempre y en todas partes. Por ejemplo, en el famoso Imperio Romano, se usaron números completamente diferentes, que ahora se usan a veces para numerar capítulos en libros, designaciones de siglos, etc. A estos números los llamamos romanos y solo hubosiete: І - uno, V - cinco, X - diez, L - cincuenta, C - cien, D - quinientos, M - mil. Con la ayuda de estos siete números, todos los demás números fueron registrados. Si una figura más pequeña estaba delante de una más grande, entonces se restó de una más grande, y si después de una más grande, se le agregó. Algunos de los mismos números se pueden repetir no más de tres veces seguidas. Por ejemplo, II es dos, III es tres, IV es cuatro (5 - 1 = 4), VI es seis (5 + 1 = 6).
Otros sistemas numéricos
Con el inicio del desarrollo de la tecnología informática, se empezaron a utilizar otros sistemas numéricos, más cerca de las máquinas que de las personas. Por ejemplo, natural para computadoras es un sistema de números binarios que consta de dos números: 0 y 1. Por ejemplo, escribimos varios números en una fila usando un sistema de números binarios: 0 es cero, 1 es uno, 10 es dos (cero unos y uno es dos) 11 - tres (una unidad y una deuce), 100 - cuatro (cero unidades, cero dos, uno cuatro), 101 - cinco (una unidad, cero dos, uno cuatro), etc. Es decir, las unidades de bits aquí son dos veces diferentes: dos, cuatro, ocho, etc.
Además del sistema de números binarios, los sistemas octal y hexadecimal ahora se usan ampliamente en computación y programación.