Hoy en día, la palabra "Integral" se puede escuchar con bastante frecuencia y, a menudo, en los lugares más inesperados, como en el canal de bolsa de valores en la televisión o en las noticias. A menudo escuchamos la frase "indicadores integrales", la palabra "integrado", "integrador" y similares. Bueno, en general, los funcionarios y los presentadores de televisión, en general, son muy aficionados a varias palabras de moda, aunque es poco probable que entiendan su verdadero significado. Y hoy hablaremos sobre qué es la integral, qué tipos de integral existen y cuáles son sus diferencias.
¿Cuál es la integral
Integral es una palabra latina que nos llegó desde la antigüedad, y significa "Todo" o "Completo". Es decir, está claro que si se dijo un objeto sobre un objeto, por ejemplo, un recipiente de leche, significaba que estaba lleno y que había tanta leche como estaba.
Con el tiempo, esta palabra comenzó a usarse en disciplinas completamente diferentes: filosofía, política, economía, álgebra y geometría. Pero la interpretación más simple de la integral está dada por las matemáticas.
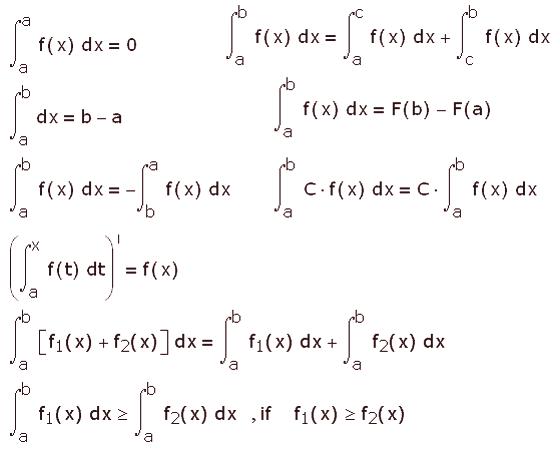
Cierta integral
Entonces, la integral es una cierta suma de partes separadas. Estos son los ejemplos más simples para una comprensión más clara de la esencia de este término:
- El sujeto es la integral (suma) de las moléculas.
- Una hoja en una celda es una integral (suma) de celdas.
- El sistema solar es la integral (suma) del sol y los planetas.
- La sociedad es una integral de las personas.
- Un segmento es la integral (suma) de metros. Si es un segmento pequeño, entonces centímetros, milímetros o segmentos microscópicos.
- ÁreaCualquier superficie es una integral de metros cuadrados, centímetros cuadrados o milímetros, y también áreas microscópicas.
- El volumen es la integral de metros cúbicos o, como también se les llama, litros.
¿Qué son las integrales definidas e indefinidas?
Comencemos por una determinada, ya que su significado es más fácil de entender.
La geometría estudia las áreas . Por ejemplo, si desea pegar papel tapiz en casa, necesita conocer el área de las paredes para saber cuánto papel tapiz debe comprar. Luego, simplemente multiplica la longitud del muro por la altura y obtén su área. En este caso, esta área es una integral de metros cuadrados o centímetros, según las unidades en las que la midió. Pero las superficies cuya área necesitamos calcular no siempre tienen la forma de un rectángulo, un cuadrado o incluso un círculo. En la mayoría de los casos, estas son formas complejas con lados ondulados. El ejemplo más común es el área de una figura debajo de una curva que tiene la ecuación y = 1 /x. El hecho es que es imposible encontrar su área usando fórmulas comunes, por lo que encontramos el área de un cuadrado, un círculo o incluso una esfera. Para ello, se desarrolló una integral definida.
La esencia del método es que nuestra figura compleja debe dividirse en rectángulos muy estrechos, tan estrechos que la altura de cada dos adyacentes es casi igual. Está claro que, de hecho, es posible reducir el grosor de estos rectángulos infinitamente, por lo que el tamaño dx se utiliza para denotar su grosor. X es la coordenada, y el prefijo d esDesignación de valor infinitamente decreciente. Por lo tanto, cuando escribimos dx, esto significa que tomamos un segmento a lo largo del eje x, cuya longitud es muy pequeña, casi cero.
Por lo tanto, ya hemos acordado que el área de cualquier figura es la integral de metros cuadrados o cualquier otra figura con áreas más pequeñas. Entonces nuestra figura, el área que estamos buscando, es la integral o la suma de esos rectángulos infinitamente delgados en los que la hemos dividido. Y su área es la suma de sus áreas. Es decir, nuestra tarea completa es encontrar el área de cada uno de estos rectángulos y luego sumarlos a todos: esta es una integral definida.
Ahora hablemos de la integral indefinida. Solo para entender de qué se trata, primero debe aprender sobre el derivado. Así que vamos a empezar.
La derivada es el ángulo de inclinación de la tangente a cualquier gráfico en algún punto. En otras palabras, la derivada es cuánto se inclina la gráfica en un lugar determinado. Por ejemplo, una línea recta en cualquier punto tiene la misma pendiente, y la curva es diferente, pero puede repetirse. Para calcular la derivada, existen fórmulas especiales, y el proceso de su cálculo se llama diferenciación. Es decir La diferenciación es la determinación del ángulo de la gráfica en un punto dado.

Tabla de integrales indefinidas básicas
Y para hacer lo contrario: para averiguar la fórmula de la gráfica por su ángulo de inclinación, recurren a la operación de integración o suma de datos sobre todos los puntos. Integración y diferenciación.Dos procesos recíprocos. Solo que aquí no usan la integral, que estaba en el primer párrafo (para determinar el área), sino la otra, la indefinida, es decir, que no tiene límites.
Supongamos que sabemos que la derivada de una determinada función es igual a 5. 5 es el ángulo de inclinación de la gráfica con respecto al eje x en un punto dado. Luego, al integrar la derivada, aprendemos que la función de esta derivada, que también se llama primitiva, es y = 5x + c, donde c es cualquier número. Para la integración, así como para la diferenciación, hay fórmulas especiales que se pueden encontrar en las tablas.
Conclusión
En conclusión, resumimos que la principal diferencia entre una integral definida y una indefinida está en sus asignaciones. Ciertas integrales se utilizan para calcular parámetros limitados, como área, longitud o volumen, e indefinido, al calcular parámetros que no tienen límites, es decir, funciones.
Video interesante sobre este tema:







